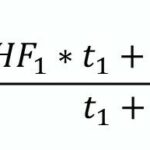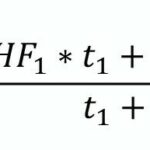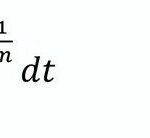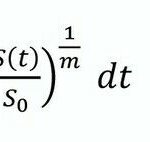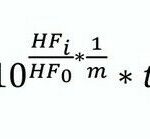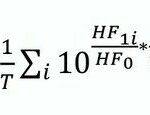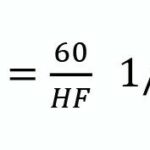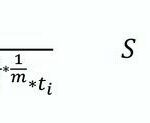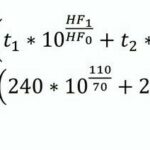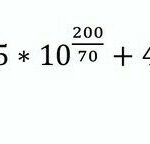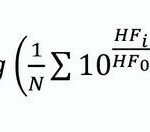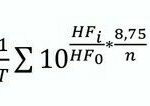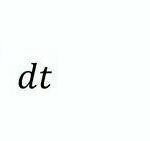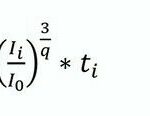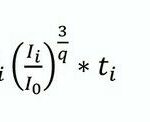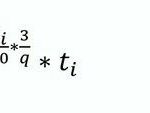1. Einleitung
Eine der Aufgaben auf dem Gebiet der Arbeitsplatzgestaltung ist es, die körperlich schwere Arbeit abzubauen. Um zu wissen, um welchen Schweregrad der Arbeit es sich handelt, ist es erforderlich, die Antwortreaktion des menschlichen Körpers auf die physische Belastung während der Arbeit zu messen, zu bewerten und zu beurteilen. Dies geschieht im Allgemeinen durch die Ermittlung von Herzperiodendauer bzw. Herzschlagfrequenz und dem Sauerstoffverbrauch über eine bestimmte Tätigkeitsdauer. Die Beurteilung erfolgt dann nach Arbeitsenergieumsatz und/oder Herzschlagfrequenz-Mittelwert.
Die vorliegende Arbeit befasst sich ausschließlich mit dem Problem der Mittelwert-Bildung sowie der Skalierung der Herzschlagfrequenz. Damit soll eine genauere Beurteilung der Schwere der Arbeit sowohl für die Gesamt- als auch für Teiltätigkeiten ermöglicht werden.
2. Problemstellung
Es ist in der Arbeitshygiene (-medizin) üblich, die telemetrisch oder nicht telemetrisch gewonnenen Herzschlagfrequenz-Werte (nachfolgend HF genannt) so aufzubereiten, dass zum Schluss der zeitlich gewogene arithmetische Mittelwert – mit oder ohne Streuung – angegeben und zur Beurteilung verwendet wird.
Wenn der arithmetische Mittelwert eine richtige Voraussetzung für eine Beurteilung ist, so muss er auch bei Grenzfällen der Belastung eine verlässliche Beurteilung ermöglichen.
An zwei Beispielen soll gezeigt werden, dass diese Aussage angezweifelt werden muss.
1. Beispiel:
Teiltätigkeit 1 mit HF1 = 110 1/min und einer Dauer
von t1 = 240 min
Teiltätigkeit 2 mit HF2 = 90 1/min und einer Dauer
von t2 = 240 min
2. Beispiel:
Teiltätigkeit 3 mit HF3 = 200 1/min und einer Dauer
von t3= 45 min
Teiltätigkeit 4 mit HF4 = 90 1/min und einer Dauer
von t4 = 435 min
Den zeitlich gewogenen arithmetischen Mittelwert berechnet man mit nachstehender Formel
Man erhält in beiden Beispielen als Ergebnis HF1,2= HF3,4 = 100 1/min.
Beide Mittelwerte ergeben bei gleicher Ruheherzschlagfrequenz (HF0) auch die gleichen Beanspruchungen, obwohl das Beispiel 2 auf Dauer eine Überlastung des normal trainierten Kreislaufs darstellt, da eine HF von 200/min über 45 min/Arbeitsschicht den Regelmechanismus des Kreislaufes überfordert.
Dieses Ergebnis widerspricht der eingangs postulierten Behauptung, dass der arithmetische Mittelwert eine richtige Beurteilung der Arbeitsschwere ermöglicht.
Die Aussage über den arithmetischen Mittelwert in obigen Beispielen ist aber nur dann zutreffend, wenn das Kreislaufregelverhalten als linear betrachtet wird.
In praxi sind jedoch aufgrund der Nichtlinearität des Kreislaufregelverhaltens die Schwankungsbreiten im Bereich der HF0 erheblich höher als im oberen Belastungsbereich. Dadurch werden die oberen und unteren Werte des Regelbereiches falsch gewichtet und das kann zusätzlich zu einer weiteren unrichtigen Bewertung der tatsächlich wirkenden Beanspruchung führen.
Dieses Problem, sowie der Einfluss der HF0, der Arbeitsdauer und der Kurzzeitbelastung auf den arithmetischen Mittelwert führen zu der Fragestellung:
Ist die Ermittlung des arithmetischen Mittelwertes der Herzschlagfrequenz eine ausreichend genaue Grundlage für die Beurteilung der Herz-Kreislauf-Beanspruchung des Menschen durch den Arbeitsprozess?
Die Beantwortung dieser Fragestellung ist das Ziel nachfolgender Überlegungen.
3. Versuch einer biologisch angepassten Wichtung bei der Mittelwertbildung
Das zu findende Verfahren muss eine sichere Beurteilung der Arbeitsschwere zulassen, auch wenn sich – wie bereits erwähnt – die Einflussgrößen HF0, Arbeitszeit und Kurzzeitbelastung, deren dynamisches Verhalten durch die Arbeitstätigkeit bedingt ist, ändern.
Zunächst sollen die Einflussgrößen diskutiert werden.
3.1 Validierung der Einflussgrößen
3.1.1 Einfluss der Ruheherzschlagfrequenz (HF0)
Der Begriff der HF0 lässt sich unterschiedlich definieren. Zwischen der biologisch „echten“ HF0 und der arbeitshygienisch verwendeten HF0 besteht oft ein beachtlicher Unterschied. Es ist z. B. dem Untersuchenden überlassen, ob er die HF0 im Liegen, Sitzen oder im Stehen misst; eine einheitliche Festlegung existiert nicht. Berücksichtigt man zudem, dass bereits die Vorbelastungen vor Arbeitsbeginn, die Vorbereitungsarbeiten für das Ankleben der Elektroden, das Ankleben selbst, die ungewohnten Fragen der Untersuchenden, trotz bester psychischer Vorbereitung der Probanden Vorstartreaktionen auslösen, die die HF0 beträchtlich erhöhen können, dann muss man sich fragen, welche Bedeutung für die Beurteilung eine solche „unzuverlässige“ untere Grenze hat.
Relativ genau, und mit verhältnismäßig geringer Streuung lässt sich der Bereich oberhalb der HF0 bis zum Bereich der Extrembelastung bestimmen. Subtrahiert man davon die HF0, so erhält man die Arbeitsherzschlagfrequenz, deren Skalierung zur Beurteilung der Arbeitsschwere führt.
Welchen Wert haben aber die Skalierung und damit auch die Bewertung der Arbeitsschwere, wenn bei ein und demselben Probanden die Ausgangslage bereits in der Größenordnung einer Arbeitschwerekategorie schwanken kann? Das kann zu der Aussage führen, dass heute die Arbeit für den Probanden als schwer eingestuft werden muss und morgen – mit anderer Ausgangslage – evtl. als mittelschwer oder sehr schwer, je nachdem in welche Richtung sich die HF0 verschiebt, obwohl die Arbeitsanforderung und damit die Belastung völlig gleichgeblieben ist.
Da derartig große Schwankungen in der Bewertung keine schnelle und sichere Aussage über die Schwere der Arbeit zulassen, müssten diese über mehrere Messungen gemittelt werden. Die auf diese Weise gemittelten intraindividuellen und interindividuellen Schwankungen bedingen aber einen beträchtlichen messtechnischen und rechnerischen Aufwand.
Es gilt daher, ein Bewertungsverfahren zu finden, dass den Einfluss der HF0 berücksichtigt, trotzdem eine sichere Bewertung der Arbeitsschwere und gleichzeitig den messtechnischen und rechnerischen Aufwand verringert.
3.1.2 Einfluss der Arbeitszeit
Nimmt man eine bestimmte Dauerleistungsgrenze des Organismus in Abhängigkeit von der Schwere der Arbeit an, so muss diese als auf eine bestimmte Arbeitszeit bezogen werden. Davon abweichende Arbeitszeiten – vor allem Überstunden – müssen zu einem anderen (niedrigeren) Dauerleistungsgrenzwert führen, da sonst physiologische Reserven angegriffen werden, die evtl. im biologischen 24 h-Rhythmus nicht wieder aufgefüllt werden können. Eine abnehmende physische Leistungsfähigkeit wäre die Folge. Die unterschiedliche Arbeitszeit und die damit verbundene Dauerleistungsgrenzenänderung müssen in einem Bewertungsverfahren ihren Niederschlag finden.
3.1.3 Einfluss der Kurzzeitbelastungen
Bei der bisherigen Bewertung, der der arithmetische Mittelwert zugrunde liegt, werden alle Belastungsintervalle gleich gewichtet und zeitlich gewogen. Man kann zwar für die HF zulässige Höchstzeiten definieren und dadurch ihre Gefährlichkeit für den Organismus dokumentieren, aber eine exakte Abhängigkeit in Form einer Funktion (HF = f(Arbeitszeit)) ist aus der Literatur nicht bekannt.
Man kann also nicht vorherbestimmen, welche zulässige HF z. B. bei 6 oder 11h Arbeitszeit nicht überschritten werden darf; oder umgekehrt, welche Arbeitszeit bedingt welche zulässige HF (s. Pkt. 5).
Ein zu findendes Beurteilungsverfahren muss so aufgebaut sein, dass ohne zusätzliche Einschränkungen ein Vergleich mit einem zulässigen Höchstwert möglich ist.
3.2 Herleitung des Verfahrens
Bei der Beurteilung der Gehörschädlichkeit von Arbeitslärm stand man vor einigen Jahrzehnten vor der gleichen Fragestellung wie o. a.: wie kann man die verschiedenen Einflussfaktoren (Lärmintensität, Einwirkdauer, Impulshaltigkeit) so in einer Formel berücksichtigen, dass letztendlich eine Einwertangabe die Wirkung der berücksichtigten Einflussfaktoren beschreibt. Das „Dresdner Gehörschadensmodell“ beschrieb retrospektiv die Beziehungen zwischen dem durch Lärm verursachten Gehörschaden (sowohl Beanspruchung als auch Bewertung und Beurteilung) und der Belastung durch Lärm. Der sog. äquivalente Dauerschallpegel (Leq) war das Ergebnis, wobei ursprünglich nicht die Energieäquivalenz im Vordergrund stand, sondern ein variabler Äquivalenzparameter (q=3…6 dB/Zeithalbierung; s.u.) die unterschiedliche Beanspruchung des Gehörs durch verschiedene Lärmaufkommen beschrieb.
Nachstehende Ableitung soll den Gedankengang dieses Verfahrens erläutern, um aufzuzeigen, dass ein ähnliches Verfahren auch für die Bewertung der HF möglich ist.
3.2.1 Herleitung des äquivalenten Dauerschallpegels
Der Ausgangspunkt dieses Verfahrens bildet Gleichung (1). Es ist dies der arithmetische Mittelwert.
I: Schallintensität
T: Gesamtzeit (z. B. Arbeitszeit) |
(t): Schallintensität als Funktion der Zeit
Durch Potenzierung mit einem sog. „Äquivalenzparameter“ (3/q) auf dessen Bedeutung unter Punkt 4.2.4. eingegangen wird) erhält man die Gleichung (2).
Mit q=3 erhält man wieder den arithmetischen Mittelwert. Mit q3 sind andere Mittelwerte möglich, die z. B. Einzelereignisse (Impulse) stärker oder schwächer als der arithmetische Mittelwert beschreiben.
Führen wir nun den Lärmpegel ein. Er ist aus bestimmten physikalischen Gründen definiert zu
wobei I0 die Bezugsintensität an der Hörschwelle ist.
Stellt man die Intensität explizit dar, so erhält man
Dividiert man GI. (2) durch I0, so lautet Gl. (5)
Nach Umformungen (Summenbildung, GI (3) in GI (5)) erhält man
Aus Gl (6) erhält man nach einfachen Umformungen Gl (7)
und schließlich mit GI(4) in GI(7) die endgültige Gleichung für den äquivalenten Dauerschallpegel Leq
Das Ergebnis dieser Gleichung für das unterschiedliche Lärmaufkommen (mit q=3) entspricht einem gewichteten Mittelwert und ist eine Einwertangabe.
3.2.2 Herleitung der äquivalenten Herzschlagfrequenz
In Analogie zu obigen Verfahren beim Lärm wird nun eine adäquate Gleichung für die Beanspruchung des Kreislaufes im Arbeitsprozess abgeleitet.
Hierbei ist der Ausgangspunkt die vom Organismus aufzubringende Energie, die ja der physischen Beanspruchung adäquat ist, wobei S(t) in Gl (9) die durch überwiegend dynamische Arbeit bedingten Energieaufwendungen darstellen.
Auch hier soll ein Äquivalenzparameter in Gl (9) eingeführt werden mit m=n/a (10), wobei a der noch zu ermittelnde Parameter /Zeithalbierung und n ein „Anpassungsparameter“ ist, wobei n=1 sein kann.
Mit GI (10) wird GI (9) zu
Mit m = 1 erhält man wieder den arithmetischen Mittelwert. Mit m 1 sind wie beim Lärm andere gewichtete Mittelwerte möglich.
Als Bezugsgröße führen wir noch eine Bezugsenergie S0 (Energieverbrauch im Ruhezustand) ein und definieren unter der Voraussetzung, dass die HF dem Energieumsatz (bedingt durch die überwiegend dynamische Arbeit) proportional ist GI (11), wobei HF0 die Ruheherzschlagfrequenz ist.
und damit wird
Führt man S0 in Gl (10) ein, so erhält man
durch Logarithmieren von Gl (13) und Umformungen findet man
Durch Einsetzen von Gl (11) in die linke Seite von Gl (14) und von Gl (12) in die rechte Seite der Gleichung (14) erhält man schließlich
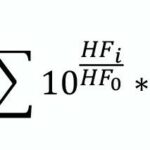
Die endgültige Formel für die gewichtete und zeitlich gewogene HF lautet:
Hierbei bedeutet:
HFeq: äquivalente Herzschlagfrequenz
T: Dauer der Arbeitszeit
Ti: Dauer der Einzeltätigkeit
HFi: Herzschlagfrequenz bei Einzeltätigkeit
m: Aquivalenzparameter
HF0: Ruheherzschlagfrequenz
Da oft die Herzperiodendauer (HPD) die Primärdaten sind, lässt sich GI (16) über
umrechnen.
Man erhält dadurch eine äquivalente Herzperiodendauer
4 Diskussion der Formeln
4.1 Was bedeutet die HFeq
Die HFeq ist — genau wie der Dauerleistungsgrenzwert – eine Einwertangabe und beinhaltet
- keine Aussage über den zeitlichen Verlauf der HF
- eine Nivellierung sämtlicher Herzschlagfrequenzunterschiede zu einem einzigen äquivalenten Wert bei gleicher Gesamtdauer (Beispielbilder s. u.)
- die Möglichkeit einer unterschiedlichen Wichtung von Teilbelastungen (Einzeltätigkeiten) je nach Wahl des Äquivalenzparameters „m“
4.2 Die Eigenschaften der HFeq
4.2.1 HFeq bei den Ausgangsbeispielen:
An den beiden Beispielen, die eingangs diskutiert wurden, soll nun gezeigt werden, wie sich die Voraussetzungen zur Beurteilung der Arbeitsschwere unter Anwendung von Gl (16) ändert (m=1).
1. Beispiel:
Tätigkeit 1: HF1 = 110 1/min mit t1 = 240 min
Tätigkeit 2: HF2 = 90 1/min mit t2 = 240 min
angenomme HF0: HF0 = 70 1/m
Arbeitszeit: T = t1 + t2
2. Beispiel:
Tätigkeit 1: HF3 = 200 1/min mit t3 = 45 min
Tätigkeit 2: HF4 = 90 1/min mit t4 = 435 min
angenomme HF0: HF0 = 70 1/min
Arbeitszeit: T = t3 + t4
Beispiel 1 ergibt unter Anwendung der Gleichung für die HFeq einen Wert, der nur wenig über den mit dem arithmetischen Mittelwert gewonnen Wert liegt (∆HFeq = 2/min). Diese geringe Differenz ist dadurch erklärlich, dass die HF-Werte nur gering schwanken.
Im Beispiel 2 beträgt die Differenz zum arithmetischen Mittelwert ∆HFeq = 35/min.
Nach diesem Ergebnis muss eine derartige belastende Tätigkeit abgelehnt werden, wenn man die übliche Beurteilung entsprechend der Skalierung der HF oder Arbeits-HF zugrunde legt. Die eingangs erwähnte Überforderung des Kreislaufregelvermögens wird durch obiges Ergebnis bestätigt.
4.2.2 Zum Einfluss HF0 auf HFeq
Das Verhalten der GI (16) bei Änderung der HF0 soll ebenfalls an den beiden eingangs diskutierten Beispielen erläutert werden. Nachstehende Tabelle 1 ermöglicht einen sofortigen Überblick:
Die (unsinnige) 1. Kommastelle wurde angegeben, um aufzuzeigen, dass im Beisp.1 eine Änderung der HF0 um (∆HF0= 20 /min keinen nennenswerten Einfluss auf die HFeq hat. Im Beisp. 2 ist dieser Einfluss bereits wesentlich größer.
Trotzdem bleiben im Ergebnis die Differenzen der HFeq bei einer Änderung der HF0 um 10/min noch unter ∆HFeg = 10/min, d.h. die Änderung der HF0 bewirkt selbst bei diesem extremen Beispiel, noch keine Änderung der Beurteilungsstufe (z. B. von schwerer auf sehr schwere Arbeit).
Somit kann man sagen, dass das im Pkt. 3.1.1. kritisierte Verhalten der HF0 bei der Beurteilung der Arbeitsschwere über die HFeq nicht mehr auftritt und dadurch eine wesentlich sichere Skalierung und Beurteilung der Arbeitenschwere möglich ist.
4.2.3 Zum Einfluss der Arbeitszeit
Die in GI (16) im Argument des Logarithmus vorhandene Zeit T, kann theoretisch jede beliebige Zeitdauer bedeuten.
Sinnvoll angewandt bedeutet T jedoch die Arbeitszeit/Schicht. Bei z. B. regulärer 12 h-Schicht muss für T also 12 h eingesetzt werden.
Hier die Berechnungen für beide Beispiele bei ausgewählten Schichtdauern (Gl (16); m=1: HF0= 70/min):
Die Werte der HFeq in den Beispielen nehmen wie zu erwarten mit steigender Arbeitszeit bei gleichbleibender physiologischen Beanspruchung ab.
4.2.4 Zur Kurzzeitbelastung:
Da in der HFeq die Zeitstruktur der HF nicht mehr enthalten ist (Einwertangabe), muss die zeitliche Dauer der Einzeltätigkeiten im Argument des Logarithmus von GI (16) berücksichtigt werden. Dies geschieht durch den Term
Die Dimension dieses Terms ist eine Zeit, die zur Gesamtzeit T (Arbeitszeit) ins Verhältnis gesetzt wird.
Aus der Lärmmesstechnik ist bekannt, dass der Leq auch über Klassierung berechenbar ist. Dies ist auch hier möglich, wobei die Klassierung z. B. durch die Multimoment-Häufigkeitsmethode bei der Erfassung der HF ersetzt werden kann.
GI (16) lautet dann
Wählt man als Multimoment-Häufigkeit z. B. folgendes Zeitraster: 27 s Totzeit und 3 s Registrierzeit, dann erhält man für diese 0,5 min einen HF-Wert, der eben für dieses Zeitintervall repräsentativ ist. Je nach Tätigkeit des Probanden sind andere Zeitraster denkbar. Definiert man nun für die gesamte Intervallbreite der HF entsprechende Klassen (z. B. mit einer Klassenbreite von 5 HF), so erhält man ein Verteilungshistogramm, dass sich nach Gl (18) auswerten lässt, wobei Ni die Anzahl der Zählungen pro HF-Klasse und N die Gesamtzahl der Zählungen bedeuten. Durch Multiplikation von Ni mit 0,5 min (gem. obigen Beispiel) ist der Zeitbezug wiederhergestellt.
4.2.5 Größe und Bedeutung des Äquivalenzparameters
In der Lärmmesstechnik wird in der Praxis bei der Leq-Bildung der Äquivalenzparameter q per definitionem mit 3 dB/Zeithalbierung angesetzt, wenn man die Gehörschädlichkeit des Lärmes beurteilen will. In Gl (8) bedeutet dies, dass sich an der Wichtung des Leq nichts ändert, wenn pro Zeithalbierung der Einwirkzeit des Lärmes sich der zugehörige Schalldruckpegel um 3 dB erhöht. Überträgt man dies auf Gl (16), so muss es für die HFeq einen Aquivalenzparameter geben, der dieselben Be-dingungen erfüllt, d.h. dass sich bei einer Halbierung der Einwirkzeit einer physischen Beanspruchung die HFi um einen bestimmten Betrag erhöht. Diesen Betrag kann man wie folgt ermitteln.
4.2.5.1 Festlegung von Grenzwerten für die HF bei schwerer Arbeit
Als Dauerleistungsgrenze für z. B. schwere Arbeit ist in der Literatur überwiegend eine HFeg = HF1 = 110 /min für eine Schicht angegeben.
Aus dem Institut für Arbeitshygiene der TU Dresden, Medizinischen Akademie * wurden dem Verfasser weitere Wertepaare für schwere Arbeit angegeben:
HF1 = 110 /min mit t1 = 480 min
HF2 = 140 /min mit t2 = 30 min
HF3 = 170 /min mit t3 = 5min
4.2.5.2 Ermittlung des Äquivalenzparameters „m“
Aus obigen drei Wertepaaren kann man unter dem Aspekt der Zeithalbierung je Stufe bei gleichzeitiger konstanter Erhöhung der HF folgende Tabelle 3 aufstellen, wobei die vorgegebenen Wertepaare nur geringfügig geändert werden.
Aus Tab. 3 lässt sich der Äquivalenzparameter a ablesen. Je Zeithalbierungsstufe darf die HF im Mittel um 8,75/min zunehmen, um die vorgegebenen Wertepaare genügend genau zu realisieren.
In m=n/a eingesetzt erhält man mit a=8,75: m= n/8,75.
Gl (16) lässt sich nunmehr präzisieren:
Wählt man n = 8,75, so erhält man den arithmetischen Mittelwert (m=1) über alle Teiltätigkeiten. Bei n 8,75 sind abweichende Mittelwertbildungen möglich, die evtl. eine bessere Anpassung an das biologische Geschehen ermöglichen.
Das Verhalten von Formel (19) ist aus nachfolgenden Beispielen ersichtlich (Tab. 4 und 5). Hier wurde zwei Belastungen (HF1 mit t1; HF2 mit t2; n=8,75; t1 + t2= 480 min) zunächst nach der üblichen Vorgehensweise (zeitlich gewogener Mittelwert so umgerechnet, das sich 5 Varianten immer mit dem gleichen Mittelwert HF = 100 / min ergeben (s. Tab 4).
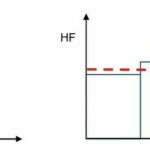
Berechnet man nun nach Formel (19) mit den o.g. Parametern die HFeq mit HF0 = 60…80 1/min (Tab. 5), so lässt sich feststellen, dass die hohen Beanspruchungen strenger bewertet werden. Das entspricht nach Ansicht des Verfassers (ohne Beweis) auch den tatsächlichen physiologischen Gegebenheiten.
Aus Tab. 5 erhellt, dass die Unterschiede der HFeg (∆maxHFeq = 5/min im Fall1) bei Änderung der HF0 vernachlässigbar sind.
Damit wurde eine der eingangs diskutierten Fehlerquellen beseitigt.
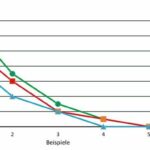
Tab. 5 bildlich dargestellt liefert folgenden Überblick: (S. Bild 1)
4.2.5.3 Einfluss des Äquivalenzparameters auf die HFeq
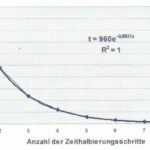
Wird die HF = f(Halbierungsschritte x) aufgetragen, dann ergibt sich mit guter Näherung eine Gerade (s. Bild 2).
Die T = f (Halbierungsschritte x) liefert eine abklingende e-Funktion. Sie lautet
Beide Funktionen können ineinander umgerechnet werden. Dies erreicht man, indem man HF = 8,75x+101,25 aus Bild 2 nach x aufgelöst und die Gleichung in Bild 3 eingesetzt wird. Nach einigen Umformungen erhält man mit genügender Genauigkeit:
Diese Gleichung gilt gem. Voraussetzung nach Tab. 3 für T = 480 min (nicht für Überstunden!)
Sind nicht die HF sondern die Herzperiodendauern (HPD) die Primärdaten, so lässt sich über die Beziehung HPD = 60/ HF die GI (21) leicht in Gl (22) bzw. Gl (22a) umrechnen
oder
Beide Gleichungen (21, 22) sind gut geeignet, um Einzelwerte der Beanspruchungen bei der Auswertung hinsichtlich ihrer Zulässigkeit zu kontrollieren. Dies ist ein wichtiger Aspekt bei der Arbeitsgestaltung, um einzelne Tätigkeiten hinsichtlich ihrer Kreislauf-Beanspruchung beurteilen zu können.
In der aufgezeigten Art und Weise lassen sich bei entsprechender Vorgabe von Grenzwerten auch für leichte, mittelschwere und sehr schwere Arbeit Kurven finden, die sich mathematisch in geschlossener Form darstellen lassen.
Vereinbarungsgemäß ist der Äquivalenzparameter — wie bereits bei der Herleitung von GI (17) erläutert – geeignet, um eine Wichtung der HFi vorzunehmen.
Die Wirkungsweise soll für m =1 (willkürlich angenommen) an beiden eingangs betrachteten Beispielen soll nun diskutiert werden. (Tabelle 6)
Die Auswertung von Tab. 6 lässt folgende Schlüsse zu:
- Die relativ starken Schwankungen der HF0 ergeben bei konstantem Äquivalenzparameter keine nennenswerten Änderungen im Ergebnis der HFeq im Beispiel 1.
Im extremen Beispiel 2 liegen die Änderungen mit jeweils ca. ∆HFeq 15 /min bei gleichem Äquivalenzparameter ebenfalls noch innerhalb einer Bewertungsstufe. - Auch, wenn der Äquivalenzparameter bei gleicher HF0 in weiten Grenzen geändert wird, gibt es kaum Änderungen im Beispiel 1. Im Beispiel 2 wird jedoch in Abhängigkeit vom Äquivalenzparameter eine deutliche Änderung erreicht.
5. Schlussbemerkungen
Ziel dieser Arbeit war es, ein bereits für die Beurteilung der Beanspruchung durch Arbeitslärm angepasstes und bewährtes mathematisches Modell auf das Kreislaufverhalten bei überwiegend dynamischer körperlicher Arbeit zu übertragen.
Die im Pkt. 2 genannten Mängel des Beurteilungssystems auf der Grundlage des arithmetischen Mittelwertes sind durch das vorgestellte Verfahren weitgehend beseitigt. Der Einfluss von Schwankungen der Ruheherzschlagfrequenz (HF), der unterschiedliche Arbeitszeiten ist eliminiert.
Dem Verfasser kommt es bei der Vorstellung beider Verfahren nur auf das Prinzip an. Jegliche Zahlenwerte beruhen auf vorgegebenen Werten aus der Literatur, zu deren statistischer Absicherung und Genauigkeit der Verfasser nichts sagen kann.
Bei einer Präzisierung der vorgegebenen Werte ist eine Validierung ohne weiteres möglich, ohne dass sich am Verfahren selbst etwas ändert.
Wenn erforderlich, kann durch Änderung des Aquivalenzparameters eine noch bessere Anpassung der Gleichungen an das Kreislaufverhalten erreicht werden.
Aufgrund der Eigenschaften der hergeleiteten Gleichungen ist eine sichere Beurteilung der Einzel- und der Gesamtbeanspruchung des Kreislaufes mit weniger Aufwand als bisher möglich.
Bei Anwendung dieses Verfahrens ist – bis auf extreme Belastungen – eine Bestimmung der Ruheherzschlagfrequenz nur noch grob erforderlich. Sie sollte jedoch nicht unbeachtet bleiben, da sie einen Überblick über den Trainingszustand des Probanden zulässt.
Damit fallen alle eingangs erwähnten Fehlermöglichkeiten bei der Bestimmung der Arbeitsschwere weg. Es ist ebenfalls nicht nötig eine Arbeitsherzschlagfrequenz zu definieren, weil allein der gemessene und gewichtete Mittelwert (HFeq) bei entsprechender Skalierung eine Beurteilung der Arbeitsschwere zulässt.
Es sei an dieser Stelle ausdrücklich betont, dass alle anderen Einflussfaktoren, die während des Arbeitsprozesses die Beanspruchung des Herz-Kreislauf-Systems beeinflussen, nicht Gegenstand dieser Betrachtungen sind.
Abschließend sei noch darauf hingewiesen, dass diese theoretische Arbeit an einigen Beispielen rechnerisch überprüft wurde. Das Ergebnis war überaus zufriedenstellend. Der Feldbeweis durch praktische Anwendung steht allerdings noch aus.
Literatur
DIN EN ISO 6385:2004–05: Grundsätze der Ergonomie für die Gestaltung von Arbeitssystemen (ISO 6385:2004); Deutsche Fassung EN ISO 6385:2004
Kraak, W, Fuder, G, Kracht, L: Die Ausbildung von Gehörschäden als Folge der Akkumulation von Lärmeinwirkungen – Teil 2 (als Manuskript gedruckt, TU Dresden)
Lühring, H. & Seibel, H.D., Arbeit und psychische Gesundheit. Göttingen, Verlag für Psychologie, 1984, S. 13 – 36
Oppelt/Vossius: Der Mensch als Regler; VEB Verlag Technik Berlin, 1970
Rohmert, W. Das Belastungs-Beanspruchungs-Konzept. Z.Arb.wiss. 38 (10 NF) 1984,193 – 200
Rohmert, Laurig: Physische Beanspruchung durch muskuläre Belastungen in: Schmidtke, H: Ergonomie, 3. Auflage 121–143,
Hansa Verlag 1992
Strasser, H: Editorial zum Themenheft „Arbeitsphysiologie“ Z.Arb.wiss. 53 (25 NF) 1999
*Herrn OA Dr. med. Naumann gebührt Dank für seine bereitwillige Unterstützung